E. A and B and Lecture Rooms
A and B are preparing themselves for programming contests.
The University where A and B study is a set of rooms connected by corridors. Overall, the University has n rooms connected by n - 1corridors so that you can get from any room to any other one by moving along the corridors. The rooms are numbered from 1 to n.
Every day А and B write contests in some rooms of their university, and after each contest they gather together in the same room and discuss problems. A and B want the distance from the rooms where problems are discussed to the rooms where contests are written to be equal. The distance between two rooms is the number of edges on the shortest path between them.
As they write contests in new rooms every day, they asked you to help them find the number of possible rooms to discuss problems for each of the following m days.
Input
The first line contains integer n (1 ≤ n ≤ 105) — the number of rooms in the University.
The next n - 1 lines describe the corridors. The i-th of these lines (1 ≤ i ≤ n - 1) contains two integers ai and bi (1 ≤ ai, bi ≤ n), showing that the i-th corridor connects rooms ai and bi.
The next line contains integer m (1 ≤ m ≤ 105) — the number of queries.
Next m lines describe the queries. The j-th of these lines (1 ≤ j ≤ m) contains two integers xj and yj (1 ≤ xj, yj ≤ n) that means that on the j-th day A will write the contest in the room xj, B will write in the room yj.
Output
In the i-th (1 ≤ i ≤ m) line print the number of rooms that are equidistant from the rooms where A and B write contest on the i-th day.
Examples
input
4 1 2 1 3 2 4 1 2 3
output
1
input
4 1 2 2 3 2 4 2 1 2 1 3
output
0 2
Note
in the first sample there is only one room at the same distance from rooms number 2 and 3 — room number 1.
----------------------------------------editorial-------------------------------
In this problem we have to answer to the following queries on tree: for given pairs of vertices your program should output number of eqidistand vertices from them.
Let's denote:
dist(a, b) as distance between vertices a and b.
depth[a] as distance between root of the tree and vertex a.
size[a] as size of subtree of vertex a.
On each picture green nodes are equidistant nodes, blue nodes — nodes from query.
Preprocessing: Read edges of tree and build data structure for LCA (it is more convenient to use binary raise, becase we will use it further for other purposes).
Complexity: O(NlogN)
Queries:
We have to consider several cases for each query:
1) a = b. In that case answer is n.
2) dist(a, b) is odd. Then answer is 0.
3) dist(a, l) = dist(b, l), where l = LCA(a, b).
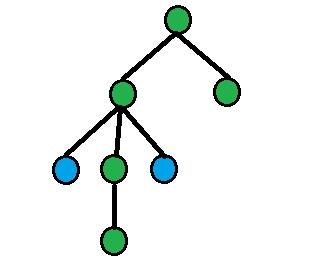
Find children of l, which are ancestors of a and b (let's denote them as aa and bb). Answer will be n - size[aa] - size[bb].
4) All other cases.
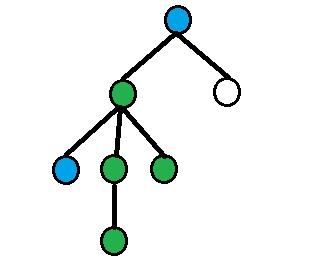

Assume that depth[a] > depth[b]. Then using binary raise find dist(a, b) / 2-th ancestor of a (let's denote it as p1), dist(a, b) / 2 - 1-th ancestor of vertex a (denote it as p2). Answer will be size[p1] - size[p2].
Complexity: O(logN) for each query, O(MlogN) for all queries.
Resulting complexity:: O(MlogN + NlogN
--------------------------------------------code--------------------------------------------------------
// tree is treated as 1 based
// level is also 1 based
#include<bits/stdc++.h>
using namespace std;
typedef long long int lli;
list<pair<int,int> >li[100010];
lli dp[100010][30];
int lev[100010];
int dist[100010];
int countt[100010];
int all;
int dfs(int start,int par,int le,int di)
{
lev[start]=le;
list<pair<int,int > >:: iterator it;
int ret=1;
for(it=li[start].begin();it!=li[start].end();it++)
{
if(it->first!=par)
{
dp[it->first][0]=start;
lev[it->first]=le+1;
dist[it->first]=di+it->second;
ret+= dfs(it->first,start,le+1,di+it->second);
}
}
countt[start]=ret;
return ret;
}
int binary_rais(int a,int b)// return lca of a,b
{
if(lev[a]<lev[b]) swap(a,b);
int lg;
for(lg=1;(1<<lg)<=lev[a];lg++);
lg--;
for(int i=lg;i>=0;i--)
{
if(lev[a]-(1<<i)>=lev[b])
{
a=dp[a][i];// moving a upward
}
}
if(a==b) return a;
else
{
for(int i=lg;i>=0;i--)
{
if(dp[a][i]!=-1 && dp[a][i]!=dp[b][i])
{
a=dp[a][i];
b=dp[b][i];
}
}
return dp[a][0];
}
}
int find(int a,int b,int gap)// return ans
{
if(lev[a]<lev[b]) swap(a,b);
if(lev[a]==lev[b]) // case 1 if both are at same distance from parent
{
int lg;
for(lg=1;(1<<lg)<=lev[a];lg++);
lg--;
for(int i=lg;i>=0;i--)
{
if(lev[a]-(1<<i)>=lev[b])
{
a=dp[a][i];
}
}
for(int i=lg;i>=0;i--)
{
if(dp[a][i]!=-1 && dp[a][i]!=dp[b][i])// moving botha and b up
{
a=dp[a][i];
b=dp[b][i];
}
}
if(a==b)
{
return all-countt[a];
}
else
return all-countt[a]-countt[b];
}
else// else shift low till (gap/2)-1 and ans will be
// no of child of par[(gap/2)-1] - no of child of (gap/2)-1
{
int shift=(gap/2)-1;
int lg;
for(lg=1;(1<<lg)<=lev[a];lg++);
lg--;
for(int i=lg;i>=0;i--)
{
if(shift-(1<<i)>=0)
{
shift-=(1<<i);
a=dp[a][i];
}
}
return countt[dp[a][0]]-countt[a];
}
}
int main()
{
int n;
cin>>n;
all=n;
for(int i=0;i<n-1;i++)
{
int a,b,c;
cin>>a>>b;
li[a].push_back({b,1});
li[b].push_back({a,1});
}
memset(dp,-1,sizeof dp);
dist[1]=0;
dp[1][0]=0;
dfs(1,-1,1,0);
int max_h=20;
for(int i=1;i<=max_h;i++)
{
for(int j=1;j<=n;j++)
{
if(dp[j][i-1]!=-1)
dp[j][i]=dp[dp[j][i-1]][i-1];
}
}
int q;
cin>>q;
while(q--)
{
int a,b;
cin>>a>>b;
if(a==b)
{
cout<<all<<endl;
continue;
}
int par= binary_rais(a,b);
int distance=dist[a]+dist[b]-2*dist[par];
if(distance%2==1)
cout<<0<<endl;
else
{
cout<<find(a, b,distance)<<endl;
}
}
}
No comments:
Post a Comment