---------------------------------------------------------EDITORIAL-------------------------------------
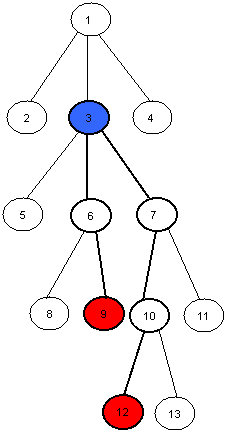
DISTANCE B/W a and b = distance b/w a and lca(a,b)+ distance b/w b ans lca(a,b),
initially we find distance of all nodes from node 1 (1 is also root of the rooted tree) now
distance of a and lca(a,b)= distance a from node 1 - distance of lca(a,b) from 1
#include<bits/stdc++.h>
using namespace std;
typedef long long int lli;
int euler[1000000],level[1000000],f_occ[1000000];
int id=0;
list<pair<int,int> > li[1000000];
int kk=0;
lli dist[1000000];
#define inf 100000000
struct st
{
int val;
int index;
} tree[1000000];
int dfs_dist(int start,int par)
{
// cout<<"start "<<start<<endl;
list<pair<int,int> >:: iterator it;
for(it=li[start].begin();it!=li[start].end();it++)
{
if(it->first!=par)
{
dist[it->first]=it->second+dist[start];
dfs_dist(it->first,start);
}
}
}
void dfs(int start,int lev,int par)
{
//if(kk++==10) exit(0);
//cout<<" start "<<start<<" "<<par<<endl;
euler[id]=start;
level[id]=lev;
f_occ[start]=min(f_occ[start],id);
id++;
list<pair<int,int> >:: iterator it;
for(it=li[start].begin();it!=li[start].end();it++)
{
if(it->first!=par)
{
// cout<<" ap "<<it->first<<endl;
dfs(it->first,lev+1,start);
euler[id]=start;
level[id]=lev;
f_occ[start]=min(f_occ[start],id);
id++;
}
}
}
st query(int node,int start,int end,int r1,int r2)
{
// if(cc++==10) exit(0);
// cout<<" start "<<start<<" end "<<end<<" range "<<r1<<" "<<r2<<endl;
if(start>end || r1>end || r2<start)
{
//cout<<" out of range "<<endl;
st ab;
ab.val=inf;
ab.index=-1;
return ab;
}
if(r1<=start && r2>=end)
{
return tree[node];
}
else
{
st q1=query(2*node,start,(start+end)/2,r1,r2);
st q2=query(2*node+1,((start+end)/2)+1,end,r1,r2);
if(q1.val<q2.val) return q1;
else return q2;
}
}
void build(int node , int start,int end)
{
if(start==end)
{
tree[node].val=level[start];
tree[node].index=start;
return ;
}
else if(start>end)
{
tree[node].val=inf;
tree[node].index=-1;
return ;
}
else
{
build(2*node,start,(start+end)/2);
build(2*node+1,((start+end)/2)+1,end);
if(tree[2*node].val<tree[2*node+1].val)
{
tree[node].val=tree[2*node].val;
tree[node].index=tree[2*node].index;
}
else
{
tree[node].val=tree[2*node+1].val;
tree[node].index=tree[2*node+1].index;
}
}
}
int main()
{
int n;
cin>>n;
for(int i=0;i<n-1;i++)
{
int a,b,c;
// for making 1 based index
cin>>a>>b>>c;
a++,b++;
li[a].push_back(make_pair(b,c));
li[b].push_back(make_pair(a,c));
}
// memset(f_occ,1000000,sizeof f_occ);
for(int i=0;i<=2*n;i++) f_occ[i]=1000000;
dfs(1,1,0);
dist[1]=0;
id--;
dfs_dist(1,0);
build(1,0,id);
/* for(int i=0;i<=id;i++) cout<<euler[i]<<" ";
cout<<endl;
for(int i=0;i<=id;i++) cout<<level[i]<<" ";
cout<<endl;
for(int i=0;i<=id;i++) cout<<f_occ[i]<<" ";
cout<<endl;*/
int q;
cin>>q;
while(q--)
{
int a,b;
cin>>a>>b;
a++;
b++;
int x1=f_occ[a];
int x2=f_occ[b];
if(x1>x2) swap(x1,x2);
//cout<<x1<<" "<<x2<<endl;
st lc=query(1,0,id,x1,x2);
int lca=euler[lc.index];
// cout<<lca<<endl;
// cout<<"dist "<<dist[a]<<" "<<dist[b]<<" "<<dist[lca]<<endl;
cout<<dist[a]+dist[b]-2*dist[lca]<<endl;
}
}
------------------------------------------------binary rais solution--------------
// tree is treated as 1 based
// level is also 1 based
#include<bits/stdc++.h>
using namespace std;
typedef long long int lli;
list<pair<int,int> >li[50010];
lli dp[50010][30];
int lev[50010];
int dist[50010];
int dfs(int start,int par,int le,int di)
{
lev[start]=le;
list<pair<int,int > >:: iterator it;
for(it=li[start].begin();it!=li[start].end();it++)
{
if(it->first!=par)
{
dp[it->first][0]=start;
lev[it->first]=le+1;
dist[it->first]=di+it->second;
dfs(it->first,start,le+1,di+it->second);
}
}
}
int binary_rais(int a,int b)// return lca of a,b
{
if(lev[a]<lev[b]) swap(a,b);
int lg;
/// maximum jump that can be alloweable to make both a and
// b at same level will be the depth of the node a
for(lg=1;(1<<lg)<=lev[a];lg++);
//
lg--;
// this will make both at same level
// we can write any number as the power of 2
// so by binary raise we can reach to any node
for(int i=lg;i>=0;i--)
{
if(lev[a]-(1<<i)>=lev[b])
{
a=dp[a][i];// moving a upward
}
}
// now a and b are at same level
// cout<<" at same level "<<a<<" "<<b<<endl;
if(a==b) return a;
else
{
for(int i=lg;i>=0;i--)
{
if(dp[a][i]!=-1 && dp[a][i]!=dp[b][i])// moving botha and b up
{
a=dp[a][i];
b=dp[b][i];
}
}
return dp[a][0];
}
}
int main()
{
int n;
cin>>n;
for(int i=0;i<n-1;i++)
{
int a,b,c;
cin>>a>>b>>c;
a++;// making 1 based ;
b++;
li[a].push_back({b,c});
li[b].push_back({a,c});
}
memset(dp,-1,sizeof dp);
// we are consedering 1 as the root of all nodes
// so its parent is non so its pow(2,0) the parent is 0;
dist[1]=0;
dp[1][0]=0;
dfs(1,-1,1,0);
int max_h=20;// or lon(n)
// maximum height
for(int i=1;i<=max_h;i++)
{
for(int j=1;j<=n;j++)
{
if(dp[j][i-1]!=-1)
dp[j][i]=dp[dp[j][i-1]][i-1];//
}
}
int q;
cin>>q;
while(q--)
{
int a,b;
cin>>a>>b;
a++;
b++;
int par= binary_rais(a,b);
cout<<dist[a]+dist[b]-2*dist[par]<<endl;;
}
}
--------------------------------------------------------------------end----------------------------------------------