Sparse Table (ST) algorithm
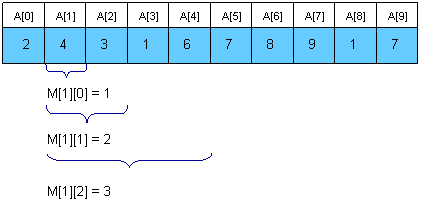
A better approach is to preprocess RMQ for sub arrays of length 2k using dynamic programming. We will keep an array M[0, N-1][0, logN] where M[i][j] is the index of the minimum value in the sub array starting at ihaving length 2j. Here is an example:
A better approach is to preprocess RMQ for sub arrays of length 2k using dynamic programming. We will keep an array M[0, N-1][0, logN] where M[i][j] is the index of the minimum value in the sub array starting at ihaving length 2j. Here is an example:
For computing M[i][j] we must search for the minimum value in the first and second half of the interval. It’s obvious that the small pieces have 2j – 1 length, so the recurrence is:
The preprocessing function will look something like this:
void process2(int M[MAXN][LOGMAXN], int A[MAXN], int N)
{
int i, j;
//initialize M for the intervals with length 1
for (i = 0; i < N; i++)
M[i][0] = i;
//compute values from smaller to bigger intervals
for (j = 1; 1 << j <= N; j++)
for (i = 0; i + (1 << j) - 1 < N; i++)
if (A[M[i][j - 1]] < A[M[i + (1 << (j - 1))][j - 1]])
M[i][j] = M[i][j - 1];
else
M[i][j] = M[i + (1 << (j - 1))][j - 1];
}
Once we have these values preprocessed, let’s show how we can use them to calculate RMQA(i, j). The idea is to select two blocks that entirely cover the interval [i..j] and find the minimum between them. Let k = [log(j - i + 1)]. For computing RMQA(i, j) we can use the following formula:
So, the overall complexity of the algorithm is <O(N logN), O(1)>.
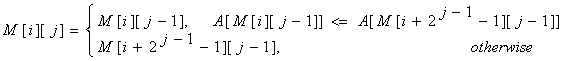

No comments:
Post a Comment